We have many papers about Knowledge graphs and how they help LLM fight hallucinations and give more accurate answers. Graphs are everywhere.
Knowledge graphs and not just graphs
Graphs are pure mathematical structures of sets of nodes and sets of pair vise nodes that are called edges. Graph theory is a critical part of mathematics and computer science. Knowledge graphs are based on the same mathematical apparatus but are all secret sources.
Knowledge graphs encode semantics that represent relations of entities. So nodes become a knowledge entity, and edge is a relationship between entities. Knowledge graphs are really industry with their own standards like RDF that allow describing a core of semantics — triples. Triple just describes a directed relation between two entities.
Strings not things
in the most simple form, RDF triple encodes a resource, and in the most simple form, a resource could have an id with attached attributes and properties. At some point, Google started a revolution of KG with their paper about things.
You could read more details about switching from labels and strings to things and complex entities.
It gives a better foundation for AI agent memories and RAG pipelines. Now, we have better tools for memory storage and knowledge enrichment.
Knowledge Graphs are not enough, and Tripples is not enough.
Now we have a complex entity that got beyond simple triple but still feet to RDF somehow
, in this brilliant article, the author raises the topic of why we need something more than just triple
So, we have a challenges specific to AI agents and AI memory
- temporal aware memory
- multi-mode and multi-lingual information
- human like multy context memory and recall
Temporal aware Semantic and Episodic memory for AI agents
one of the big topics is encoding time and time-dependent information in knowledge graphs.
Time is complex concept for encoding. Graphs have a multiple strategies to encode time in graphs
- snapshots
- node history
- validity quintuples
- messages and changes
- event streaming
More in article
The task becomes more complex when we consider time as semantic information rather than just a part of the data structure.
Semantically, time is even more complex and requires complex data structure.
You could go deep dive into my article
Hypergraphs as rescue
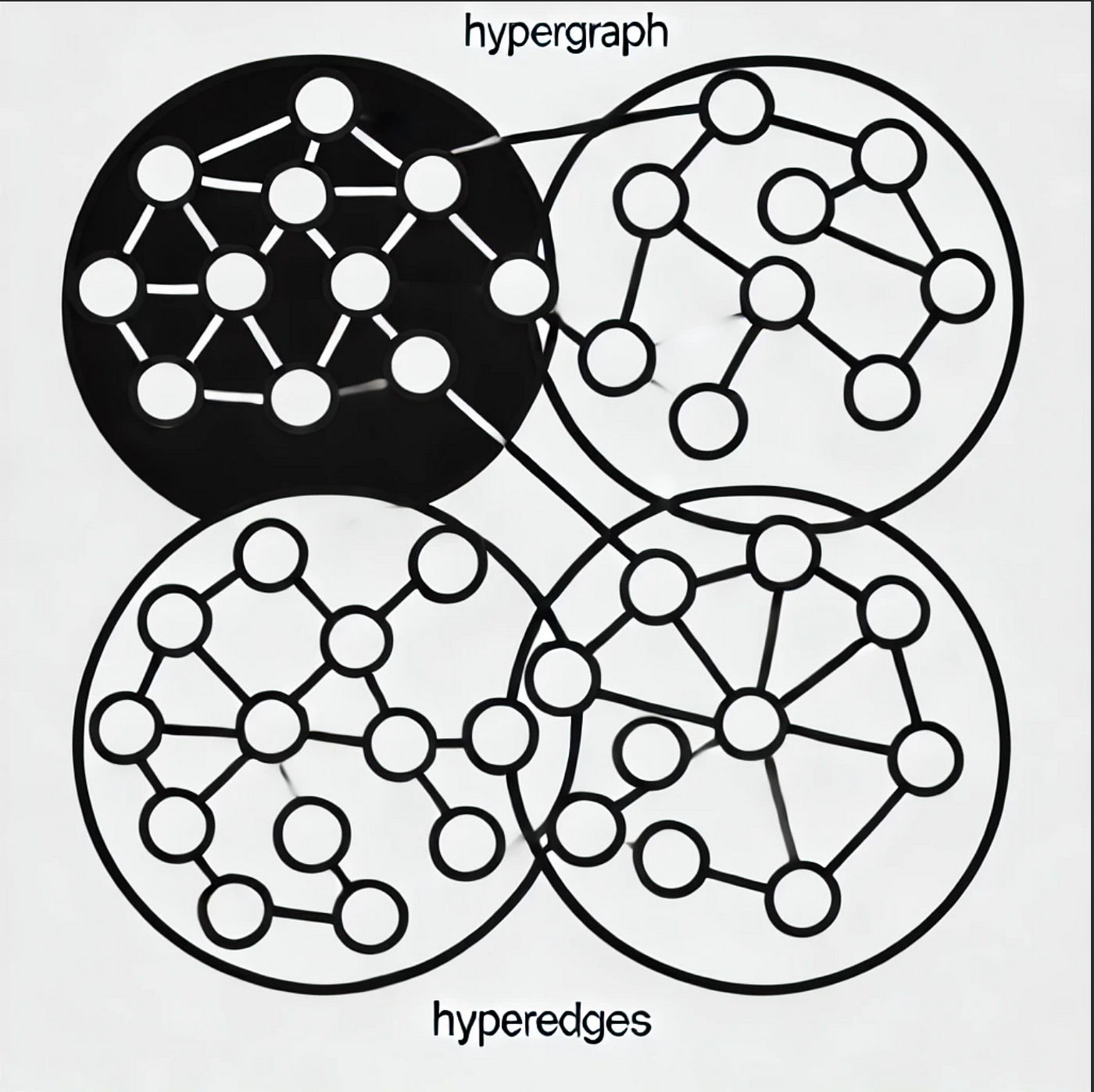
Hypergraphs are a mathematical generalization of graphs where edges contain sets of nodes. We can create edges that connect multiple nodes and organize nodes as time-dependent or context-dependent edges.
You can read my article to see hypergraphs on action and learn how to persist them.
Named Graphs and Graph of Graphs for Multi-model and multilingual data
Hypergraphs allow us to create and organize complex relations as edges, enabling us to encode time or context. Mathematically, hyper edge allows us to manage a set of nodes, but sometimes, we need the ability to organize nested context or more hierarchical dependencies. In this case, hypergraphs are not a rescue.
Named graphs allow us to have a NESTED subgraph hosted in a node. So you could have multilevel graphs.
You could see how to model them
We could simply introduce a location property to a node, or as an option, we could allow multiple locations to a node. It gives the possibility to have nodes and subgraphs in different contexts
Now we have instruments for
- Multi-lingual and multi-mode encoding
- time aware encoding
Humman-like memories for AI Agent with Metagraph
The last and biggest challenge is a human-like memory with multiple contexts and buckets of memory stored in a complex network of neuron relations. A graph of Graphs could help, but it is still luck in representing human memory complexity.
A meta graph is a further abstraction or generalization that allows us to treat relationships themselves as first-class entities. Essentially, a meta graph extends the idea of a graph by considering graphs about graphs—it allows nodes and edges to contain complex information, often other graphs, thereby enabling hierarchical structures.
Hierarchical Representation: In metagraphs, both nodes and edges can represent simple entities and other graphs or complex relationships. This helps model meta-level relationships, where relationships can be nested.
Flexible Relationships: Metagraphs allow higher-order reasoning. You can represent both nodes and edges as graphs, enabling a multi-level structure where different types of relationships and entities can exist at different levels of abstraction.
A node in a metagraph represents a single node or an entire subgraph. The key difference between a Metagraph and a Graph of Graphs is edges and paths. Meta Edge is a set of nodes and also a set of edges. The most crucial metapath is not a sequence of edges. It is a set of edges where the source and target are nodes.
Nowadays, metaphors are the most closed data structure that allows the model of the complexity of human-like memory. Unfortunately, databases and storage don't work effectively and natively with meta graphs or hypergraphs.